>律動論
Vol.1 音符のなりたち
拍(はく)とは、「打つ」という意味をもっています。
手拍子を1回打つ間隔を1拍(いっぱく)と数えます。
また、メトロノーム(クリック)の1回の発音が1拍になります。
音の長さは、音符(おんぷ)を使って表わします。
音の長さとは楽音が鳴りひびいている時間のことで、これを歴時(れきじ)、音長などといいます。
その長さには、長いものから短いものもまであり、さまざまの楽音の長さを目で見てわかるように書き表わしたものが音符です。
通常では四分音符を1拍として基準にすることが多いため、
ここではそれぞれの音符の長さを四分音符の長さと比較して表していきます。
ではまず音符の表し方を紹介しましょう。
音符は、下の図のように、符頭(ふとう)と、符尾(ふび)と、鈎(こう)(かぎ)で成り立っています。
符尾を上側にのばしたものと、下側にのばしたものがあり、状況によって使い分けています。

① 符頭
音符を書くとき、まずは、たまを書きます。
このたまを、符頭(ふとう)と呼びます。
符頭には、白たま(たまを書き、中を塗りつぶさない符頭)と、黒たま(黒く塗りつぶした符頭)があります。
後で紹介しますが白たまは二分音符以上の比較的長い音のときに使われます。
バンドのアレンジのときにも長く伸ばした音を白たまといって使ったりもします。
符頭は、楽譜上の五線の上、または線と線の間に書きます。
② 符尾
符頭の左から下に向けて立てられる棒、または符頭の右から上に立てられる棒を符尾(ふび)と呼びます。
ただし全音符(1小節ぶんの長さを表す音符)には符尾は付きません。
音符の符尾を上に向けて書くか下に向けて書くかにもルールがあります。
符頭が第三線(五線のちょうど中央にある線)よりも上側に置かれているときには符尾を下に向けて書き、
符頭が第三線よりも下側に置かれているときは符尾を上に向けて書きます。
符頭がちょうど第三線の上にのっているときは、上下のどちらに向けてもよいことになっています。
和音(2つ以上を同時に鳴らした音)に符尾をつける場合には、
和音を構成している音の中で第三線から最もはなれた位置にある音を基準に考えます。
第三線から最もはなれた位置にある音が第三線(五線のちょうど中央にある線)よりも上側に置かれているときには符尾を下に、
符頭が第三線よりも下側に置かれているときは符尾を上に向けて、
その符尾で全部の音をまとめてしまいます。
二度音程(CとDなどの1音違い)またはこれを含む和音の場合、
符頭をそのままならべてしまったら重なってしまって読みにくくなってしまいます。
こういった場合には二度音程の高い音の方を右側に書き、低い音の方を左側に書きます。
今の例ではDの音を少し右側にずらして書き、Cの音を少し左側にずらして書くのです。
これによって重なることなく読みやすい楽譜になります。
この和音に符尾を立てるときには、符尾はその中央に書くことになります。
長さのちがう音符の和音は、共通の符尾でまとめずに、それぞれに別々の符尾を用います。
一つの譜表に高音部分と低音部分を分割して表す場合は、
パート(声部)を区別するために、高音部分の符尾を上向きに、低音部分の符尾を下向きに書きます。
歌唱部分や、ドラム譜などによく見られます。
③ 鈎
四分音符よりも短い長さの音は符尾の先に羽をつけ、この羽の付けられる本数で音の長さを区別します。
この羽を鈎(こう)(かぎ)といいます。
鈎は符尾を上下どちらに立てた場合でも、かならずその先端から右側に付きます。
鈎の付いた音符が2個以上続くとき、それらを別々に書くかわりに太い横線で結んで1つにまとめる方法を用います。
鈎をつなげて旗(はた)のようにしてしまうのです。
このまとめかたですが、音符を連結させる旗は拍子を理解しやすくするために
1拍ごと、1小節ごと、小節の半分ごとを1つの組にしてまとめます。
つまり拍の途中から次の拍までを旗でまとめたり、2拍目から3拍目にかけて旗でまとめたり、
小節をまたいで旗でまとめたりすることはしません。
もちろん高さの違う音でも鈎をまとめて旗にすることができます。
高さの違う音の鈎を旗でまとめた場合、符尾を上向きに書くか下向きに書くかにもルールがあります。
旗でひとまとめにした音符のうち、第三線よりも高い音と低い音の数をくらべます。
第三線よりも高い音が半数以上の場合は符尾を下向きにそろえて書きまとめ、
第三線よりも低い音が半数以上の場合は符尾を上向きにそろえて書きまとめるのです。
Vol.2 音符の種類
① 単純音符
まず、四分音符の長さを基準にして、さまざまな長さを持つ音符を表していきます。
この四分音符を基準に、その2倍、4倍、または1/2倍、1/4倍、1/8倍、1/16倍の長さを表す音符があります。
これらの音符は、ある一つの音符(四分音符の場合が多い)を基準として、
その倍、さらに倍などのように、2を掛けていったもの、または、半分、半分の半分などのように、2で割っていったもので、
単純音符(たんじゅんおんぷ)とよばれます。
| 音符 | 名称 | 音の長さ | |
| 全音符 | 4分音符の4倍 または1小節の長さ |
||
| 2分音符 | 4分音符の2倍 | ||
| 4分音符 | ----- | ||
| 8分音符 | 4分音符の2分の1 | ||
| 16分音符 | 4分音符の4分の1 | ||
| 32分音符 | 4分音符の8分の1 | ||
② 付点音符
単純音符では、基準となる音符の3倍、または1.5倍などの長さを表すことができませんでした。
このような場合には符頭の右側に小さな点を1個付けて、基準となる音符の1.5倍の長さを表すことができます。
この小さな点を付点(ふてん)といい、付点のついた音符を付点音符(ふてんおんぷ)といいます。
付点は、基準となった音符の1/2の長さを表しています。
そして、これをもとの音符に加える事により、実際には基準となる音符の1.5倍の長さを表すことになります。
例をあげてみると、四分音符に付点をつけた場合、
付点は四分音符の半分の長さである八分音符を意味しています。
そして、この八分音符をもとの四分音符に加えた長さが付点四分音符の長さになります。
| 音符 | 名称 | 音の長さ | |
| 付点2分音符 | |||
| 付点4分音符 | |||
| 付点8分音符 | |||
| 付点16分音符 | |||
③ 複付点音符
付点を2個付けることによって基準となる音符の7/4の長さを表すことができます。
このように2個の付点を付けたものを複付点音符(ふくふてんおんぷ)といいます。
2個の付点のうち、第1の付点では基準となる音符の1/2を表し、
第2の付点では、第1の付点の表す長さの1/2、つまり基準となっている音符の1/4の長さを表します。
ですから、基準となる音符に、1/2の長さと、1/4の長さを加え、実際には、基準となる音符の7/4の長さを表すことになります。
例をあげてみると、ニ分音符に付点を2つつけた場合、
1つめの付点はニ分音符の半分の長さである四分音符を意味していて、
2つめの付点は四分音符の半分の長さである八分音符を意味しています。
これらを全部足した長さが複付点ニ分音符ですから、
複付点ニ分音符はニ分音符の長さ+四分音符の長さ+八分音符の長さということになります。
| 音符 | 名称 | 音の長さ | |
| 複付点2分音符 | |||
| 複付点4分音符 | |||
| 複付点8分音符 | |||
Vol.3 音の長さを変える記号
付点のほかにも、音の長さを変える記号があります。
① タイ/tie
付点を使わなくても、タイを使用すれば、単純音符とはちがった長さを表わすことができます。
タイ/tie(連結という意味)は、それぞれの音符を切らずに一続きの長さにする記号で、
符頭と符頭を弧線(こせん)でつないで表します。
ですから、2個以上の同じ高さの音符をひと続きにしようとするときには、
それらの音符の符頭をタイで結合することによって長さを伸ばすことができます。

② 連符
ある音符の長さを任意の数に等分し、それらを一連にしたものを、連符(れんぷ)といいます。
三連符(さんれんぷ)は、これらの連符の中でもっとも多く使用されていて、
一連の等分された3個の音符に分割記号(ぶんかつきごう)、または単に数字の3を付けて表します。
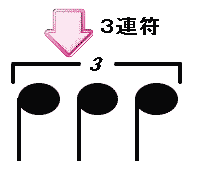
まず、基準となる長さの音符の半分の長さの音符を3個まとめて三連符を作ります。
上の図の例では4分音符をまとめて連符を作っているので、
もとの長さ(基準となっている長さ)は2分音符であることが言うことができ、その長さを3等分していると意味しています。
2分音符の長さを連符を使って分割するとき、その半分の長さの音符(つまり4分音符)をまとめて書き表していくのです。
同じように4分音符の長さを連符を使って分割するときには、その半分の長さである8分音符をまとめて書き表すのです。
3連符の他にも、1個の音符を5等分、6等分、7等分した五連符、六連符、七連符などがあります。
Vol.4 休符の種類
音符とは逆に楽音の中で無音(音がない状態)の長さを表わしたものを休符(きゅうふ)といいます。
全音符と同じ長さの無音状態は全休符であらわし、
二分音符と同じ長さの無音状態は二分休符、四分音符と同じ長さの無音状態は四分休符などのように
音符と休符がそれぞれ表わす長さは一致するように定まっています。
また、休符には単純音符に相当する長さの休符だけではなく、付点音符・複付点音符に相当するものもあり、
呼び方も同じように付点休符(ふてんきゅうふ)、複付点休符(ふくふてんきゅうふ)などといいます。
しかしほとんどの場合は付点休符、複付点音符は使用しないで、単純に休符を2個以上組み合わせて書き表してしまいます。
| 休符 | 名称 | 音の長さ |
| 全休符 | 4分休符の4倍 または1小節の長さ |
|
| 2分休符 | 4分休符の2倍 | |
| 4分休符 | 4分音符と同じ長さの休符 | |
| 8分休符 | 4分休符の2分の1 | |
| 16分休符 | 4分休符の4分の1 | |
| 32分休符 | 4分休符の8分の1 |
全休符の長さは、全音符の長さに相当します。
ニ分休符の長さは、二分音符の長さに相当します。
これらは、中を塗りつぶした小さい長方形で書き表します。
この長方形の上側の辺を第四線(五線のうち、低いほうから4番目の線)に付けて、
下側の辺を第三線(五線のうち、中央のある線)に付けないようにしたものが全休符です。
逆に、長方形の上側の辺を第四線から離し、下側の辺を第三線に付けたものが二分休符です。
四分休符の長さは、四分音符の長さに相当します。
全休符の1/4の長さになります。
第二線上(五線のうち、下から2番目の線)から書き始めて、
第四間(五線のうち下から4番目の線と最も上の線との間)で書き終わります。
八分休符の長さは、八分音符の長さに相当します。
全休符の1/8、四分休符の1/2の長さになります。
第三間(五線のうち下から3番目の線と下から4番目の線の間)から書きはじめて、第二線上で書き終わります。
十六分休符、三十ニ分休符などは、八分休符の形をもとにして書いていきます。
付点休符の付点は第三間(五線のうち下から3番目の線と下から4番目の線の間)に書きます。
休符は音符とはちがい、音の高さが存在しません。
休符は形のちがいによって表す長さに差をつけてあるだけなのです。
休符は、連符の中に用いることもできます。
連符の中に存在する音符と同じ長さを表す休符を用い、音符と休符とを組み合わせて、さまざまな形を作ることができます。
すべて休符は、その小節の中で拍子の単位となる拍を表わすように置かなければなりません。
要するに、拍の途中から次の拍をまたぐ休符を使用してはならないということです。
1小節全体を休むときは、何拍子であっても全休符を用いて表します。
ですから三拍子の場合であっても付点二分音符を用いないで全休符を用いるわけです。
全楽器が同時に突然休止することを総休止(そうきゅうし)、またはゲネラールパウゼ/Generalpauseといい、
1小節全体を休止する全休符と、この略語のG.P.(ゲー・ペー)で表します。
またこの場合、全休符の上にフェルマータ/fermataという記号を添えることもあります。

Vol.5 拍と拍子
拍(はく)とは、手拍子を1回打つ間隔で、メトロノーム(クリック)の1回の発音が1拍になります。
拍を連続して鳴らしていると、実際には同じ強さの音を鳴らしていても、
不思議なことに強い拍と弱い拍が、ある一定の間隔で並んでいるように聞こえてきます。
これは、人間の感覚によるものらしく、聞こえてくる並び方は民族などにも影響されています。
これによって、拍に強弱(アクセント)の変化が生まれ、それが規則正しく並ぶのです。
楽音の強弱の規則正しい繰り返しを拍子(ひょうし)といいます。
音楽は、拍子を土台にして成り立っています。
このように、アクセントが一定の間隔をおいて規則正しく繰り返されるものを、拍節的リズム(はくせつてきリズム)ともいいます。
現在の大部分の音楽は、このリズムに基づいて作られています。
アクセントが不規則に表われる定量リズム(ていりょうリズム)や、
一定のアクセントがなく楽音の長さがそれぞれ全く無関係な自由リズム(じゆうリズム)もあります。
強く聞こえる拍は、強拍(きょうはく)または下拍(かはく)といい、アクセントのある音(強い音)を表します。
また、弱く聞こえる拍は、弱拍(じゃくはく)または上拍(じようはく)(アウフタクト/Auftakt)といい、
アクセントのない音(弱い音)を表します。
強拍と弱拍との組み合わせにはさまざまなものがあります。
この組み合わせが、何拍をひとまとまりにして繰り返されているかということを示すのが拍子です。
このひとまとまりになった拍数をとって「何拍子」といいます。
ニ拍子と三拍子は、強拍と弱拍の配置がもっとも単純で、それがあらゆる拍子の基本になっています。
そのため、これらの拍子を単純拍子(たんじゅんびょうし)といいます。
例外として、二拍子を複合したものが四拍子(※詳しくは後で説明)ですが、
その強拍、中強拍、弱拍の配置が、他の拍子の基本となるので、これも単純拍子の中に入ります。
これら以外の拍子は単純拍子をもとにして構成されているので複合拍子(ふくごうびょうし)といいます。
別の表現ではありますが、2の倍数で表される二拍子、四拍子、六拍子などを偶数拍子(ぐうすうびようし)といい、
3と、その3倍で表わされる三拍子、九拍子を奇数拍子(きすうびょうし)といいます。
また、拍子にはこれらのほかに奇数拍子と偶数拍子とを複合した
特殊拍子(とくしゅびょうし)、または混合拍子(こんごうびょうし)があります。
特殊拍子は楽曲全体ではなく一部分(1小節から数小節程度)に用いて楽曲を印象付けるために使われることが多くなります。
楽曲の拍子を示すためには拍子記号(ひょうしきごう)を用います。
拍子記号は、楽曲の最初に分数の記号で表記します。
分数の分母(-の下側)は、どの音符の長さを1拍としたかを表します。
四分音符を1拍とした場合には分母を4と記入し、八分音符を1拍とした場合には分母を8と記入します。
そして、分数の分子(-の上側)は何拍子かを表します。
楽曲の拍子は、この分数の通りに「○分の○拍子」といいます。
4分の4拍子と2分の2拍子は同じじゃないかって思うかもしれません。
しかし、4分の4拍子は1拍の長さを四分音符で表した4拍子で、
2分の2拍子は1拍の長さをニ分音符で表した2拍子ですから、
このふたつは別のものだということができます。
Vol.6 リズムのための記号
① 縦線
音符が並んでいるだけでは、どの音符が強い音でどの音符が弱い音であるかの判断をつけることが非常に難しくなります。
最初から順番に数えてみなければ強弱の区別をつけることができないのです。
そこで、拍子(楽音の強弱の規則正しい繰り返し)ごとに縦線(じゅうせん)で区切ることによって音の強弱を区別しやすくします。
この縦線と縦線とで区切られた間隔を小節(しょうせつ)といいます。
この縦線には、単縦線(1本の縦線)と、複縦線(縦線を組み合わせたもの)があります。
複縦線には拍子を区切ること以外にも意味があります。
たとえば楽曲の最後には、左が細くて右の太い複縦線を書きます。
この複縦線を終止線(しゅうしせん)といいます。
楽曲の途中で拍子、調、速度などを変更する場合は、その場所に細い2本の縦線を用いて変更する位置を示したりします。

② アクセント
拍のアクセントは、くさび形のしるしを符頭の上に付けて表します。
このしるしはアクセント記号といって、この記号の場所によって強拍の位置を表します。
アクセント記号は同じ音符に複数個つけることができ、この記号の個数によって音の強さの程度を表します。

③ リピート
それぞれの拍子は、楽曲中ずっと繰り返して使われます。
繰り返しを意味する記号として、反復記号(はんぷくきごう)(repeat/リピート)があります。
反復記号は、それにはさまれた部分を繰り返す、という意味を持った記号です。
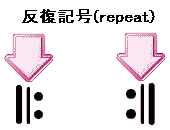
では次は、拍子の種類について紹介します。
Vol.7 単純拍子
先ほど紹介した単純拍子(たんじゅんびょうし)です。
単純拍子は全ての楽音で基本となる拍子で、二拍子、三拍子、四拍子の3種類があります。
<二拍子>
ニ拍子は強拍と弱拍が交互に繰り返されるものをいいます。
1拍の単位になる音符をかえる事により、四分のニ拍子、ニ分のニ拍子、一分のニ拍子、八分のニ拍子などを作ることができます。
二分のニを表す拍子記号は「¢(半円を意味する記号)」を用いることがあります。
二分の二拍子を、alla breve アラブレーヴェともいいます。
<三拍子>
三拍子は、強拍の後に弱拍が2回繰り返される拍子をいいます。
強拍、弱拍、弱拍という形になるわけです。
二拍子は規則正しい拍子ですが、三拍子は、ゆるやかに流れる優雅な拍子です。
三拍子の中では、四分の三拍子がもっとも多く用いられていますが、ニ分の三拍子や、八分の三拍子などもあります。
<四拍子>
四拍子は、二組の二拍子が組み合わされたもので、
後側の二拍子の強拍は、先側の二拍子の強拍よりもやや弱くなります。
このように、複数の強拍が存在する場合で、強迫よりもやや弱い強拍を中強拍(ちゅうきょうはく)といいます。
四拍子の中では、四分の四拍子(しぶんのしびょうし・よんぶんのよんびょうし)がもっとも一般的で、
拍子記号として「C」が用いられることもあります。
このほかに、八分の四拍子や、ニ分の四拍子なども使用されます。
二分の四拍子を表わすために「¢」、「¢¢」が用いられることもあります。
Vol.8 複合拍子
では、これら単純拍子を組み合わせて、二拍子、三拍子、四拍子以外の拍子を作ってみましょう。
二拍子、三拍子、四拍子以外の拍子を複合拍子(ふくごうびょうし)といいます。
複合拍子とは単純拍子を組み合わせて作られたもので、さまざまな種類が存在します。
<六拍子>
六拍子は、三拍子が2個組み合わされたもので、後側の三拍子の強拍が、中強拍になっています。
六拍子の中には、八分の六拍子、四分の六拍子などがあります。
では、ここで拍を細分化(さいぶんか)について紹介します。
言葉の言い方が難しいかもしれませんが、
たとえば四分音符を八分音符2つに分解するなどのようにして
全体としての長さは変えずに1拍を複数の音符に区切るという意味です。
<拍を二つに細分化する>
強拍を二つに細分化すると、先側が強拍、後側が弱拍になります。
また、弱拍を二つに細分化すると、先側は弱拍だったのですが、
後側がさらに弱い音になるので、見かけの上では、先側が中強拍、後側が弱拍のようなアクセントになります。
| → | ||
| → | ||
| → |
<拍を三つに細分化する>
強拍を三つに細分化すると、最初が強拍、後の二つが弱拍になります。
また、弱拍を三つに細分化すると、最初は弱拍だったのですが、後の二つがさらに弱い音になるので、
見かけの上では、最初が中強拍、後ろ二つが弱拍のようなアクセントになります。
| → | ||
| → | ||
| → |
<拍子のアクセントの比較>
では六拍子の話にもどります。
三拍子を細分化して六拍子を作った場合と、
二拍子を細分化して六拍子を作った場合の違いを図で書いて比較してみました。
| 六拍子 | |
| 三拍子 | |
| 二拍子 |
ここで四分の三拍子を例にとって考えてみましょう。
四分の三拍子の四分音符を細かくして八分音符で表した場合、1小節内に6個の八分音符を持つことになります。
しかし拍を細分化すると、分けた後の2つの音符のうち後側の音符は弱拍よりもさらに弱い音になります。
このときそれぞれの音の強弱をみてみると、すぐ上の図の三拍子のならび方になっていることがわかると思います。
それに対して八分の六拍子は、すぐ上の図でも紹介しましたが六拍子のならび方です。
図を見比べてみると四分の三拍子と八分の六拍子とではアクセントの位置が異なることがわかるでしょう。
逆に、四分のニ拍子の各拍子を三連符にした場合、八分の六拍子とアクセントの位置が同じになります。
このことから、六拍子は三拍子が2個組み合わされたものではあるが、
先側と後側の三拍子がそれぞれ1個の拍にまとまり、これが強拍と弱拍の関係になって、二拍子のアクセントになるといえます。
<九拍子>
九拍子(くびょうし)は、3組の三拍子を合わせたもので、
最初の三拍子の第1拍は強拍、第2の三拍子と第3の三拍子の強拍は中強拍になります。
九拍子の中には四分の九拍子、八分の九拍子、十六分の九拍子などがあります。
<十二拍子>
十二拍子(じゅうにびょうし)は、三拍子を4個組み合わせたもので、
各三拍子の第1拍は下の図のようなアクセント関係を構成します。
2回目と4回目の三拍子の第1拍は、中強拍よりもやや弱い次中強拍になります。
十二拍子には、四分の十ニ拍子、八分の十二拍子、十六分の十ニ拍子などがあります。
今までは二拍子を何個かセットにして新しい拍子を作ったり、三拍子を何個かセットにして新しい拍子を作ったりしました。
では、二拍子と三拍子を組み合わせてみましょう。
Vol.9 特殊拍子
特殊拍子とは、奇数拍子と偶数拍子とを複合したもので、
二拍子と三拍子とを組み合わせた五拍子、三拍子と四拍子とを組み合わせた七拍子などがあります。
また、2つの拍子を複合したものだけではなく、
3つ以上の拍子を複合した、八拍子、十拍子、十一拍子、十五拍子などもあります。
特殊拍子においても、複合拍子と同じように、前側の拍子と後側の拍子に強弱の関係があります。
2つの拍子を組み合わせた特殊拍子では、先側の拍子と後側の拍子が二拍子と同じように「強」・「弱」の関係になっていて、
先側の拍子は強く、後側の拍子はやや弱くなります。
このため、先側の拍子と後側の拍子の第1拍のアクセントをくらべてみると、
先側の拍子の強拍の方がより強い音になっています。
また、3つの拍子を組み合わせた特殊拍子では、
最初の拍子と後側2つの拍子が三拍子と同じように「強」・「弱」・「弱」の関係になり、
4つの拍子を組み合わせた特殊拍子では、
4つのそれぞれの拍子が四拍子と同じように「強」・「弱」・「中強」・「弱」の関係になります。
しかし、これらのことを理由に弱く表現される拍子の第1拍であっても、
拍子単位で考えた場合に第1拍であることには変わりないため、
特殊拍子の中に部分的に含まれる四拍子の中の中強拍よりは強いものとなります。
このことにより、同じ特殊拍子でも奇数拍子と偶数拍子との組み合わせる順序によってアクセントの位置を変化させることができ、
いろいろなアクセントの種類を持った拍子を作ることができます。
特殊拍子の拍子記号は、まず、単純拍子や複合拍子と同様に分数で表します。
そして、その右側に括弧(かっこ)を付け、分母は同様に、どの音符の長さを1拍としたかを書きます。
分子には組み合わせた拍子を、組み合わせた拍子の順序通りにたし算の形で書き表します。
拍子をいうときは、通常通りに「○分の○拍子」といいます。
もしくは、括弧の中の分数を読んで、「○分の○+○拍子」といいます。
<五拍子>
五拍子(ごびょうし)とは、二拍子と三拍子を組み合わせたものですが、
この2つの拍子を組み合わせる順序によってアクセントの位置が異なります。
二拍子を先に、三拍子を後に並べた(2+3)拍子の場合、3拍目が中強拍になります。
逆に、三拍子を先に、ニ拍子を後に並べた(3+2)拍子の場合、4拍目が中強拍になります。
| (2+3)拍子 | |
| (3+2)拍子 |
<七拍子>
七拍子(ななびょうし)とは、三拍子と四拍子を組み合わせたものです。
三拍子と四拍子を組み合わせたものと、二拍子を2つと三拍子を組み合わせたものがあります。
| (3+4)拍子 | |
| (4+3)拍子 | |
| (2+3+2)拍子 |
<それ以外の特殊拍子の例>
五拍子、七拍子以外の例を下にあげていきます。
八拍子、十拍子、十一拍子、十五拍子などがあります。
また、二拍子、三拍子、四拍子を組み合わせる事により、無限に特殊拍子を作ることができます。
| (2+3+3)拍子 | |
| (3+2+3)拍子 | |
| (3+3+2)拍子 | |
| (4+3+3)拍子 | |
| (3+4+3)拍子 | |
| (3+3+4)拍子 |
Vol.10 拍子記号
では、これらの拍子を拍子記号を使ってあらわしてみましょう。
拍子記号は通常、分数を用いて表します。
分数の分母は1拍と定義する音の長さを表し、分子は何拍子であるかを表します。
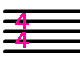 |
4分音符を1拍と定義し、4拍子を意味する |
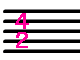 |
2分音符を1拍と定義し、4拍子を意味する |
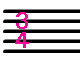 |
4分音符を1拍と定義し、3拍子を意味する |
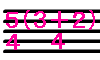 |
4分音符を1拍と定義し、5拍子(3+2拍子)を意味する |
楽曲の途中で拍子を変更する場合、
単縦線、または複縦線の上に、変更後の拍子記号を括弧で囲んで表記します。
もしくは、縦線の右に変更する拍子記号を書いて表します。
2種類の拍子を、1小節ごと交互に繰り返す場合は、2種類の拍子記号を、順に並べて記入します。
下に例をあげた拍子は四分の七拍子のようにも考えられますが、
各小節の最初の拍はどれも強拍であるため、四分の七拍子とはいえません。
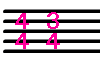
Vol.11 弱起とシンコペーション
楽曲の開始は、かならずしも拍子の第1拍で開始するというものではありません。
拍子の途中の何拍目からでも楽曲を開始することができるのです。
このようにして第1拍以外の拍で開始する場合を弱起(じゃっき)といいます。
弱起をすることにより最初の小節は拍数が不足することになります。
また、弱起の影響により最後の小節も拍数が不足することがあります。
こういった拍数の不足した最初と最後の小節を不売全小節(ふかんぜんしょうせつ)といいます。
実際には不足分の拍数は休符と考えることもできます。
逆に、拍子の第1拍で開始するものを、強起(きょうき)といいます。
拍子の中の強拍と弱拍の位置を入れかえることは、楽曲においてよく用いられます。
強拍と弱拍の位置を入れかえる方法はおもに3種類あります。
第1の方法は、一組、または連続した数組の部分の強拍と弱拍を全て入れかえる方法です。
この方法は、二拍子、四拍子において小節単位、または小節内の部分的に用いることができます。
第2の方法は、三拍子において「強」・「弱」・「弱」のうち
「強」のアクセントの位置を第2拍、または第3拍に移動させる方法です。
第3の方法は、弱拍の音と、それに続く強拍の音とが同じ高さのときに、これらをタイで結合してひと続きの長さにする方法です。
これによって、タイで連結する前の弱拍の位置にアクセントが付き、強拍に変わります。
また、連結する前の強拍はアクセントを失って弱拍に変わります。
この方法は、同じ小節の中だけでなく、縦線をはさむ小節と小節との間においても構成することができます。
逆に、強拍の音とそれに続く弱拍の音とをタイで結合した場合、アクセントの位置は変わりません。
これらの方法によって、アクセントを移動させたものを、シンコペーション/syncopationといいます。
楽曲の途中でシンコペーションが現れると規則正しい強弱の繰り返が突然変わるので、
それまでの拍子の感じとは全く別のものになります。
前の小節から食って入ることをシンコペーションと勘違いしているバンドマンも多いのですが、
強拍と弱拍の位置が入れ替わった状態がシンコペーションです。
前の小節から食って入ること以外にも、いろいろな方法でシンコペーションが作れますね。
Vol.12 リズムの定義
リズムの定義について紹介します。
一つの拍は、これをいろいろの長さの音符に分割することができます。
これによって、同じ拍子においても、音符の組み合わせを変えたものが、多く存在する事になります。
ある一定の時間の中で行なわれる、さまざまな音符の組み合わせ(または、その繰り返し)を、
リズム/rhythm、または節奏(せっそう)といいます。
拍子によって、規則正しいアクセントの繰り返しが決まり、
それをもとにして、その上に長短さまざまの音の組み合わせ(リズム)をのせていきます。
テンポ/tempo(楽曲の速度を意味します)によっても、リズムの選び方はちがってきます。
たとえば、速い楽曲では、リズムをあまり細かく分割することはできません。
逆に、ゆるやかな楽曲では、リズムの変化がとぼしいと単調になってしまいます。
また、テンポが速くなると、中強拍のアクセントは、見かけ上は消失します。
このため、複合拍子は単純拍子のように聞こえるようになります。
逆に、テンポがゆるやかになると、いままでの弱拍にもアクセントがあるように聞こえてきます。
このため、拍を細かく分割することにより、単純拍子は複合拍子に変化したように聞こえます。
以上のことより、リズムの繰り返しで楽曲が作られていきます。
ですから、リズムは音楽の性格を決定する最も重要な要素であるといえます。
拍を、さらに細かい音符に分割した場合、分割されたそれぞれの音符の強弱を表すためにも、アクセント記号を使用します。
Vol.13 拍法
では、次はリズムのとり方です。
リズムのとり方にも様々な方法があります。
リズム(拍子)の取り方を、拍法(はくほう)といいます。
手拍子を取ったり、机の上を指先などでたたいたりして、手でリズムを取る方法を、打節法(だせつほう)といいます。
また、つまさきでゆかを踏むなどして、足でリズムを取る方法を、踏節法(とうせつほう)といいます。
そして、これらの方法を用いて拍子の単位となる拍を打つことを拍子打ち(ひょうしうち)といい、
音符の長さ通りにリズムを取ることをリズム打ち(リズムうち)といいます。
一・二・三や、タン、タ、ターァのような言葉を声に出して、拍子やリズムを取る方法を、
呼節法(こせつほう)、またはリズム唱といいます。